List of Most Widely Used Probability Concepts in Data Science

Probability is one of the core components of data science, along with mathematics, computer science, and programming languages. So, succeeding in a data science career is built upon a solid foundation in these concepts. In this article, we will be focusing on probability concepts that are used in data science.

A recent Gallup survey shows 12 % of U.S. workers use AI daily and nearly 25 % use AI several times a week, especially in the tech and finance sectors. Be it understanding uncertainty in real-world data, building predictive models, or evaluating outcomes, different probability concepts are used in almost every stage of a data science project lifecycle.

Whether you are working with machine learning, statistical inference, or data-driven business decisions, you need to have a strong understanding of probability so that you can reason logically under uncertainty.

Common Probability Concepts Used in Data Science

The following are some of the common and most widely used probability concepts in data science that you need to learn to grow in your data science career.

• Random Variables

  A random variable is the numerical representation of the outcome of a random process. It is used to model uncertain quantities such as customer behavior, sensor readings, or stock prices. Two main types of random variables are:

  • Discrete random variables – Take countable values
    • Example: The number of clicks on an ad or the number of customers visiting a website page in an hour
  • Continuous random variables – Take values over a continuous range
    • Example: Engagement time on a website

  They are the basis for probability distributions and modeling real-world data mathematically.

• Probability Distribution

  Probability distributions describe how the values of a random variable are distributed. Probability distribution is the core of data analysis, statistical modeling, and machine learning.

  The following are commonly used distributions in data science:

  • Normal distribution (Gaussian distribution) – it is used to measure natural phenomena

    

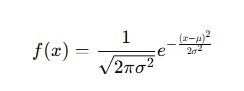
    Example: Distribution of exam scores

  • Binomial distributions – It models the number of successes in 𝑛 independent trials.

    

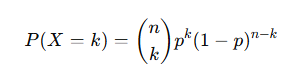
    Example: Number of users clicking an ad out of 100 visitors.

  • Bernoulli Distribution – It is used for measuring binary outcomes

    P (X=x) = px (1−p) 1−x

    Example: Whether an email is spam (1) or not (0).

    • Poisson distribution – it models the frequency of events over time or space
    • Uniform distribution – it assumes all outcomes have equal chances to appear

    By properly understanding distributions, you can choose appropriate models and make assumptions about data behavior.

• Conditional Probability

  It is used to measure the probability of an event occurring when another event has already occurred. It is expressed by:

  

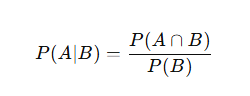
  Example: What is the probability a user buys a product (A) given they clicked an ad (B)?

  In data science projects, this is used for:

  • Feature dependencies
  • Risk assessment
  • Recommendation systems
  • Predictive modeling

  Algorithms like probabilistic models rely on conditional probability.

• Bayes’ Theorem

  Bayes’ theorem is among the most widely used probability concepts in data science. It is used to describe how to update the probability of a hypothesis depending on new evidence.

  The formula looks like this:

  𝑃 (𝐴|𝐵) = {𝑃 (𝐵|𝐴) ⋅ 𝑃 (𝐴) 𝑃 (𝐵)} / P (B)

  Example (Spam Detection):

  • A: Email is spam
  • B: Email contains the word “offer.”

  This theorem can be applied in various applications, such as:

  • Spam filtering

  • Medical diagnosis models

  • Fraud detection

  • Bayesian machine learning models

  Bayes’ theorem helps data science professionals to refine predictions as new data becomes available.

• Expectation and Variance

  Expectation or expected value represents the average outcome of a random variable over several trials. Whereas, variance means how much the data deviates from the mean.

  • Expectation is used for model evaluation, risk analysis, and optimization

    E(X) =∑x ⋅ P(X=x)

    Example: If a user spends $10, $20, or $30 with probabilities 0.2, 0.5, and 0.3, respectively, the expected spend helps businesses forecast revenue.

  • Variance and standard deviation help measure uncertainty and volatility

    Var(X)=E[(X−μ)2]

    Example: If two machine learning models have the same accuracy, the one with lower variance is considered to be more reliable.

    This probability method is used to understand how data is spread and how reliable a model is.

• Central Limit Theorem (CLT)

  This states that the distribution of sample means follows a normal distribution irrespective of the original data distribution, provided the sample size is large.

  This probability concept is used in application areas like:

  • Confidence interval estimation
  • Hypothesis testing
  • Statistical inference, etc.

  It helps data scientists apply the normal distribution assumption to non-normal data as well.

• Law of Large Numbers

  This law states that if the number of observations increases, the sample mean nears the true population mean.

  This concept is widely used for:

  • Justifying the use of large datasets
  • Explaining why models perform better with more data
  • Supporting reliable estimation and experimentation

  It is the basis for popular practices like A/B testing and analysis based on simulations.

Final thoughts!

Probability is the main pillar of data science. Be it modeling uncertainty with random variables or making informed predictions with Bayes’ theorem, the concepts of probability are used across various applications in the data science lifecycle.

By learning these probability concepts and their applications with the best data science certifications, you can improve the analytical accuracy of the model as well as strengthen data-driven decision-making.

Frequently Asked Questions

• Why is probability important in data science?

  In data science technology, probability is used to manage uncertainty, make predictions, and evaluate outcomes, especially when working with incomplete or noisy data.

• Is Bayes’ theorem necessary for machine learning?

  Yes, Bayes’ Theorem is widely used in probabilistic models, classification algorithms, and decision-making systems that update predictions based on new data.

• Do data scientists need advanced probability knowledge?

  Data scientists are expected to have a strong understanding of core probability concepts. If they are looking to advance in their data science careers, then they must look for advanced topics for specialized roles like machine learning research or statistical modeling.